浅析分形与混沌及其相关性

打开文本图片集

【摘要】 混沌与分形是20世纪一个新兴的学科理论，分形和混沌在很多自然学科和人文学科被普遍发现，非线性科学有了相当大的突破.本文主要介绍了分形与混沌的产生背景，以及分形与混沌的特征，分别对分形与混沌举出例子，对分形与混沌的相关性进行了简单介绍.

【关键词】 混沌;分形;相关性

一、

（一）分形的定义

分形的概念是美籍数学家Mandelbrot首先提出的.分形理论的数学基础是分形几何学，我们都知道线是一维的，面是二维的，立体图形是三维的，分形理论更加趋近复杂系统的描述（也就是分数维情况），更加符合客观事物的多样性与复杂性.1967年，Mandelbrot在论文中说道，海岸线是不规则的，并且具有极其复杂的变化，用一把直尺去测量海岸线的长度，只能用直线来得出近似值，当用更小的直尺去测量细小之处，并且这些地方也是曲线.1975年，他创立了分形几何学（Fractal Geometry）.在此基础上，形成了研究分形性质及其应用的科学，称为分形理论.但到目前为止还没有明确的定义.

（二）分形的特征

称集F是分形，则F具有下列性质：

1.F具有精细的结构，也就是说有人以小比例的细节.

2.F是不规则的，以至于不能用传统的几何语言来描述.

3.局部和整体的自相似性，可能是近似的或是统计的.

4.维数一般是分数，并且大于它的拓扑维数.

5.分形虽然具有复杂的结构，但是以简单的方法定义，可能由迭代产生.

（三）分形的例子

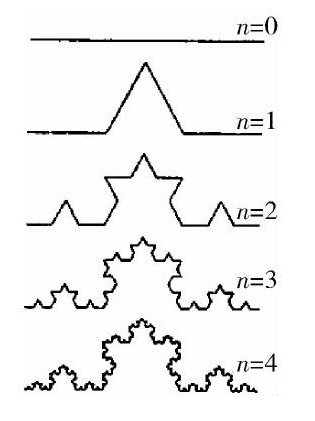
Koch曲线：1904年，瑞典数学家柯赫构造了“Koch曲线”几何图形.Koch曲线大于一维，具有无限的长度，但是又小于二维.

Koch曲线的生成过程：三次Koch曲线的构造过程主要分为三步：第一步，画出一个初始图形——一条线段;第二步，将这条线段的中间 1 3 处向外折起;第三步，按照第二步的方法依次把各段线段中间的 1 3 处向外折起.

其图构造过程如右图所示（迭代了5次的图形）.这样无限的进行下去，最终即可构造出Koch曲线.

其實分形的例子还有很多，如三分康托基、康托尘、Sierpinski垫等.自然界中也存在着分形的例子，例如，天空中的云朵、植物叶子的形状、岩石裂缝等.这些图形或者例子都存在着自相似性，复杂的图形是由一个非常简单的方程通过初值选择反复迭代得到的结果.

二、

（一）混沌的定义

简单来说，在非线性科学中，混沌是一种确定的但不可预测的运动状态，因为这些运动状态都是相似的，比表面上似乎可以确定它的运动状态及运动轨迹，又说它是不可预测的，是因为会受到外界条件的影响，造成了运动的不稳定性.混沌理论认为在混沌系统中，初始条件十分微小的变化，经过不断放大，对其未来状态会造成极其巨大的差别.

我们也可以用数学语言来定义混沌：

设V为一个集合，f：V→V称为在V上是混沌的.如果

（1）f对初始条件的敏感依赖性.

（2）f是拓扑传递的.

（3）周期点在V中是稠密的.

（二）奇异吸引子

奇异吸引子是反映混沌系统运动特征的产物，也是一种混沌系统中无序稳态的运动形态.目前奇异吸引子仅仅是一个抽象数学概念，还没有完善的理论模型.

（三）混沌的特征

1.对初值条件的敏感依赖性.

2.极为有限的可预测性.

3.混沌内部的有序性.

（四）混沌的例子

天气问题：近半个世纪以来，研究者发现许多自然现象即使可以化为单纯的数学公式，但是其行径却无法预料.如气象学家Edward Lorenz发现简单的热对流现象能引起非常大的气象变化，产生了所谓的“蝴蝶效应”.60年代，美国数学家Stephen Smale发现某些物体的行径经过一些规则性变化之后，并没有规律可循，呈现失序的混沌状态.

军事问题：马蹄铁上一个钉子是否会丢失，本是初始条件的十分微小的变化，但其“长期”效应却是一个国的存与亡.这就是军事中的所谓“蝴蝶效应”.

三、分形理论和混沌理论的联系

从总体上讲，二者在产生时并无关系，两者的关系先要从它们各自产生的背景来看，混沌的产生更多是从物理方面得来的，比如，自然界中的天气变化，分形更多是从数学中几何方面研究中总结出来的，例如，千变万化的分形图案.

混沌的主要特征初值敏感性（俗称“蝴蝶效应”）和奇异吸引子，简单来说句是确定性的非线性系统中出现的一种随机现象，随机性和确定性往往不能同时存在，混沌的奇妙之处在于把确定性和随机性给统一了.分形的核心是自相似，对很多表面无规则的复杂现象，特别是在时间和空间上存在无穷迭代非线性系统，具有很强的描述能力，这其中包含了混沌现象.分形的奇妙之处在于表面好似无规则、碎片状的东西，其实也是有规律的.

至于二者为什么紧密相关，因为它们研究的系统都是现实的非线性系统，它们有着共同的来源是动力系统，混沌吸引子就是分形，混沌是时间上的分形，分形是时间上的混沌.混沌主要讨论非线性动力系统的不稳定，发散的过程，但系统总是收敛一定的吸引子，这与分形的自相似性非常相像，可以说混沌系统与分形结构都具有自相似性.

【参考文献】

[1]周作领.符号动力系统[M].上海：上海科技教育出版社，1997.

[2]谢和平，张永平，宋晓秋，等.分形几何：数学基础与应用[M].重庆：重庆大学出版社，1991.