基于小波分解和相空间重构的大气电场混沌特征浅析

打开文本图片集

摘要： 本文通过对伴有闪电过程的地面大气电场强度时间序列进行相空间重构分析知，闪电时段内地面大气电场强度时间序列均呈现混沌特性，而非闪电时段内地面大气电场强度时间序列并不全部呈现混沌特性；闪电时段内的地面大气电场强度时间序列经过小波函数sym5的4层分解重组的低频部分的相空间重构混沌特性较原始时间序列的相空间重构混沌特性明显。

Abstract： Through the phase space reconstruction analysis knowledge， lightning period ground atmospheric electric field intensity time series showed a chaotic characteristics， rather than during the period of lightning ground atmospheric electric field intensity time series does not show chaotic characteristics of accompanied by lightning ground atmospheric electric field intensity time series； within the period lightning ground atmospheric electric field intensity time series through the four layer wavelet sym5 decomposition reorganization of the low-frequency part of the phase space reconstruction of chaotic characteristics than the original time series in the phase space reconstruction of chaotic characteristics significantly.

关键词： 小波分解；相空间；电场强度；混沌

Key words： wavelet decomposition；phase space；electric field intensity；chaos

中图分类号：TN249 文献标识码：A 文章编号：1006-4311（2016）28-0161-03

0 引言

贵州地处云贵高原亚热带地区，受西南季风的影响，雷暴活动较频繁。贵州省年平均雷暴日51.66d以上，雷电地闪平均密度达10.4次/km2，贵州属于强雷暴区域。大气对流模型具有典型的混沌特性，且雷暴天气是典型的大气强对流模型。混沌时间序列已广泛应用于大气科学类研究，混沌时间序列是介于随机和规律之间，短期内系统的运动轨道是可以预测的。黄显高[1]等人在1999年利用小波多尺度分解算法实现了噪声与混沌的分离，在此基础上他又利用小波多尺度分解实现混沌和掩藏在其中的目标信号的分离[2]。

本文数据来源于贵州省内安装的DNDY型大气电场仪测量的地面大气电场强度值，该大气电场仪有效探测半径为10km，安装在距离地面0.7m的高度。每秒采集一次数据。在实际测量的过程中，由于采集方法和仪器精度的限制，使得信号序列不可避免地夹杂噪声。小波分解是将时间序列分解为低频部分与高频部分，即将噪声的能量分布在全部的小波系数上，而信号的小波系数仅集中于频率尺度空间的有限部分，信号的能力分布在小部分的小波系数上[3]。

本文首先对DNDY型大气电场仪监测的闪电时段与非闪电时段地面大气电场强度时间序列判断是否具有混沌特征，其次对闪电过程中地面大气电场强度时间序列进行小波分解，对小波分解重组后的地面大气电场强度时间序列低频部分判断是否具有混沌特征。希望该方法对分析地面大气电场强度时间序列提供一种新思路。

1 基本理论

1.1 小波分解原理

小波分解旨在解决信号频域和时域的矛盾，采用时间窗和频率窗可变的分析方法，使得高频部分具有较低的频率分辨率，低频部分具有较高的频率分辨率。分解的小波系数进行权重处理并对小波信号进行重构。根据文献[3]，本文采用sym5小波对地面大气电场强度时间序列进行分解。

具体步骤如下：①选定一种小波，对一维时间序列进行N层小波分解；②选择一个阈值对不同尺度下的高频系数进行软阈值量化处理；③小波分解后的系数进行小波逆变换，得到分解后的重构信号。

1.2 相空间重构理论及非线性动力学特性参数算法

Takens定理[4]：采用相空间重构的延迟坐标法，利用单一的标量时间序列进行重构。

其中，n为相点数，m为嵌入维数，τ为时间延迟。选取合适的τ和m能够保障相空间重构的质量，确保预测的精准度。

混沌系统的基本特点是系统对初始值极其敏感性，两个相差无几的初值所产生的轨迹，随着时间的推移按指数方式分离，LE指数就是定量的描述这一现象的量。相关研究结果表明：在混沌研究中并不需要计算序列的所有LE指数，而只需要计算出最大LE指数即可。若最大LE指数大于零，则判断系统存在动力学混沌。本文计算最大LE指数步骤如下：

2 地面大气电场强度时间序列混沌特性识别

2.1 原始时间序列计算非线性动力学特征参数

目前分析非线性时间序列的主要方法有求算功率谱、关联维数、最大LE指数等。其中功率谱法是通过定性描述混沌特性，而关联维数d及最大LE指数则是通过定量的方法描述非线性时间序列的混沌特性。LE指数的和表征了椭球体积的增长率或减小率，最大LE指数大于零，说明不止一个指数大于零，系统就会呈现混沌特性。

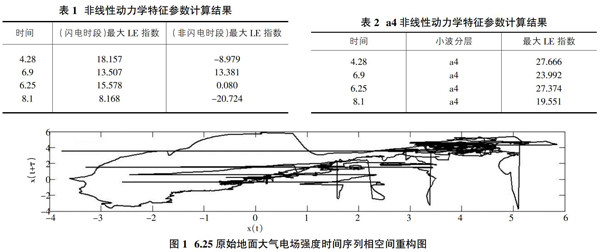
在MATLAB内部函数的基础上，根据上节理论知识编程计算，地面大气电场强度非线性时间序列的最大LE指数，若最大LE指数大于零，则该非线性时间序列具有混沌特性。因闪电过程中物理过程变化的复杂性，闪电过程中地面大气电场强度变化趋势不能用简单的线性函数拟合其变化过程。因此采用前面编制的程序对贵州省内几次伴有闪电过程的地面大气电场强度时间序列计算非线性动力学特征参数结果见表1。

通过上述计算发现，非闪电时段内非线性动力学特征参数最大LE指数有负数有正数，闪电时段内非线性动力学特征参数最大LE指数均大于零。即在非闪电过时段地面大气电场强度变化时而呈现混沌特性，时而不呈现混沌特性。且由于非闪电时段内非线性动力学特征参数最大LE指数小于零，此时系统属于耗散系统；在闪电过程中，地面大气电场强度变化均呈现混沌现象。

2.2 时间序列经小波分解后计算非线性动力学特征参数

由于噪声的存在，对采集的地面大气电场强度时间序列进行直接分析存在很大的困难。另外由于混沌信号特有的宽带性和似噪声性特征，研究混沌信号中的噪声效应成为解决问题的关键。

文献[3]中介绍了通过小波分解的地面大气电场强度时间序列低频部分不仅能够很好的反映地面大气电场强度变化的主要趋势，而且能够很好的保留闪电过程中地面大气电场强度的突变特性。为进一步了解闪电过程中地面大气电场强度时间序列的混沌特性是否明显。本文将闪电时段的地面大气电场强度时间序列进行小波分解，对其低频部分计算非线性动力学特征参数。

由于小波分解后重构会引起累积误差[4]，根据文献[3]提供的方法计算出地面大气电场强度时间序列功率谱主要集中于0.05Hz以下，得出本文可采用4层小波分解法。

根据本文1.2提供的算法，分别对经小波分解重组的闪电时段内地面大气电场强度时间序列（低频部分）a4计算非线性动力学特征参数结果见表2。

通过表2计算最大LE指数结果可知，对闪电时段内的地面大气电场强度时间序列进行小波分解后，重组的低频部分a4仍然均呈现混沌特性。经过小波分解重组后的地面大气电场强度时间序列（低频部分）计算的最大LE指数均大于原始地面大气电场强度时间序列计算的最大LE指数。即经过小波分解重组后的地面大气电场强度时间序列（低频部分）的混沌程度高于原始地面大气电场强度时间序列的混沌程度。（如图1、2所示）

3 结论

本文对伴有闪电过程的地面大气电场强度时间序列进行非线性混沌特征分析，利用matlab编程计算重构相空间的时间延迟τ、嵌入维数m、关联维数d以及最大LE指数等特征参数。通过计算发现，伴有闪电过程地面大气电场强度变化在闪电时段内均呈现混沌特性，在非闪电时段内并不是全部都呈现混沌特性。经过sym5小波分解重组后的地面大气电场强度时间序列（低频部分）的混沌程度高于原始地面大气电场强度时间序列的混沌程度。地面大气电场强度时间序列低频部分将随机噪声降低，最大LE指数波动降低，即地面大气电场强度时间序列低频部分混沌特性较原始地面大气电场强度时间序列更为明显。由于混沌时间序列是介于随机和规律之间，短期内系统的运动轨道是可以预测的，因此经过小波分解重组的地面大气电场强度时间序列（低频部分）在短期内的变化是可以预测的，为临近雷暴预报提供了一种新的思路。

参考文献：

[1]黄显高，徐健学，何岱海，等.利用小波多尺度分解算法实现混沌系统的噪声减缩[J].物理学报，1999，48（10）：1810-1817.

[2]HUANG Xianggao，XU Jianxue，HUANG Wei etal.Unmasking chaotic mask by a wavelet multiscale decomposition algorithm. Int.J.Bif&Chaos，2001，11（2）：561-569.

[3]李艳，王振会，陈红兵，等.基于小波技术的地面大气电场数据处理[J].气象科学，2012，32（2）：177-181.

[4]Takens F.Determing strange attractors in turbulence[J].Lecture Notes in Math，1981，89（8）：366-381.